MIT linear algebra course note

08/11/2017 lecture 1 & 2
1. permutation matrix
2. inverse matrix E*E-1 = I
3. identity matrix
4. 如何做矩阵变换。E*A=B 使得 第二行substract 第一行

08/12/2017 lecture 3&4
4种方法计算矩阵乘法：
1. 正常法，每个值都是1 row * 1 column
2. column way. A乘以B的每个column
3. row way. A的每个row 乘以B
4. A的每个column 乘以 B的每个row。加在一起
5. cut matrix into blocks。 然后把每个block之间进行运算

A的左逆 矩阵和右逆矩阵是相同的 if matrix is invertible (non singular)

Singular case (no inverse)
比如[1,3;2,6]

singular matrix can get 0 by some matrix x
Ax = 0 if A is singular matrix. x 是存在的

A times B的一列j，得到的是结果的C的一列j
A的一行j times B,得到的是结果的C的一行j

Gauss - Jordan (solve 2 equations at once)
[A,I]--->[I,A-1]




AB 的逆矩阵 = B-1A-1

矩阵的转置
(A-1)t = (At)-1
A 的逆矩阵的转置是A的转置的逆矩阵
A= LU
if there is no row exchange, the multiplers will directly go into L

how many operations on n *n matrix?
n^3

permutation:
可以在单元矩阵中变换

原矩阵乘以这个矩阵(permuatation matrix)表示第二行第三行互换

permutation matrix ： p-1 = pt 如果第二行和第三行 换了，那么再换一次第二行和第三行就是还是原来的矩阵

置换矩阵（Permutation matrix）：矩阵的每一行和每一列的元素中只有一个1，其余元素都为0。（不严谨的解释）

转置矩阵（Transpose matrix）：矩阵的行变成对应的列，矩阵的列变成对应的行。（不严谨的直白解释）

性质：置换矩阵(P)的逆是其（置换矩阵自己的）转置(T)，

即：P^(-1)= P^T

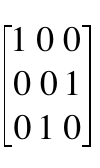
如：3×3的置换矩阵群（共3! = 6个，补充4×4的置换矩阵共4! = 4×3×2×1 = 24个）

1 0 0 | 0 1 0

0 1 0 | 1 0 0

0 0 1 | 0 0 1

----------------

0 0 1 | 1 0 0  

0 1 0 | 0 0 1 

1 0 0 | 0 1 0 

置换矩阵的逆=置换矩阵的转置（上面4个置换矩阵的转置矩阵都是自身，又因为他们的逆=他们的转置，所以他们的逆=自身）

0 1 0 | 0 0 1 

0 0 1 | 1 0 0 

1 0 0 | 0 1 0 

置换矩阵的逆=置换矩阵的转置（这两个矩阵的转置=对方，因此这两个矩阵的逆=对方）

LU分解

LU分解是指，把矩阵分解为 消元矩阵E 的逆操作 L（下三角）

和 A 被消元后的结果矩阵 U（上三角）的乘积.

• LU分解不借助 行交换的关键是是 中间不能出现 0 pivot
• 但是对最后一个 pivot 没有 非0的要求
• 因为奇异矩阵也有LU分解
• 
  

http://blog.csdn.net/qq_25834201/article/details/59748093
http://blog.csdn.net/lc013/article/details/52244464
https://github.com/mebusy/notes/blob/master/dev_notes/LinearAlgebra.md