A-1 = 1/det(A)*Ct
C 是A的 余子式矩阵
克莱默法则
Ax=b
x=A-1b = > 1/det(A)*Ct*b
计算量超级大
行列式的值相当于某个物体的体积
detA = volume of a box
先从一个单位立方体开始 => det(cube) = 1
然后不同方向stretch. 或者变形之类的。可以看看其他的tutorial.
Monday, August 28, 2017
Sunday, August 27, 2017
linear algebra lecture 18 & 19 08/27/2017
lecture 18
行列式 det A |A|
性质:
1.
det I = 1
det singular matrix = 0
2.
exchange rows reverse the sign of det.
det Permutation matrix = -1/ 1 根据单位矩阵来的
|a b
c d | = ad-bc
3.
|ta tb
c d| = t |a b; c d|
4. if two rows are equal, the det is 0.
5. subtract l*row i from row k. det doesn't change (消元的感觉)
6. row of 0s => det A = 0
7.三角矩阵的det 是对角线的乘积
8. det A = 0 if when A is singular
9.
det AB = detA*det B
det A-1 = 1/det A
det A2 = (det A)2
det 2A= 2^n*det A
(like a volume)
10. |At| = |A|
|Ut*Lt| = |LU|
=>|Ut|*|Lt| = |L|*|U|
lecture 19
det A = sum (A1aA2b...Anw)
如果 a,b...w可以通过偶数次变换成为1,2,。。。n 那就是正数,
余子式:行列式中指定一个数,去掉所在行和所在列的剩余矩阵是其中一个余子式
cofactor
行列式 det A |A|
性质:
1.
det I = 1
det singular matrix = 0
2.
exchange rows reverse the sign of det.
det Permutation matrix = -1/ 1 根据单位矩阵来的
|a b
c d | = ad-bc
3.
|ta tb
c d| = t |a b; c d|
4. if two rows are equal, the det is 0.
5. subtract l*row i from row k. det doesn't change (消元的感觉)
6. row of 0s => det A = 0
7.三角矩阵的det 是对角线的乘积
8. det A = 0 if when A is singular
9.
det AB = detA*det B
det A-1 = 1/det A
det A2 = (det A)2
det 2A= 2^n*det A
(like a volume)
10. |At| = |A|
|Ut*Lt| = |LU|
=>|Ut|*|Lt| = |L|*|U|
lecture 19
det A = sum (A1aA2b...Anw)
如果 a,b...w可以通过偶数次变换成为1,2,。。。n 那就是正数,
余子式:行列式中指定一个数,去掉所在行和所在列的剩余矩阵是其中一个余子式
cofactor
Wednesday, August 23, 2017
linear algebra 08/23/2017 lecture 17
标准正交Q为什么好
QTQ = [q1t;q2t...]*[q1,12...]= [1,0...] 单元矩阵
projection matrix
P = Q(QtQ)-1Qt = QQt (=1 if Q is square)
gram-schmidt 正交化
QTQ = [q1t;q2t...]*[q1,12...]= [1,0...] 单元矩阵
projection matrix
P = Q(QtQ)-1Qt = QQt (=1 if Q is square)
gram-schmidt 正交化
Tuesday, August 22, 2017
Monday, August 21, 2017
linear algebra lecture 14 & 15 08/21/2017
lecture 14:
正交:
row space and null space 正交 orthogonal 因为A*x = 0
column space and null space of At 正交
Xt*y=0
subspace S is orthogonal to subspace T means that every vector in S is orthogonal to every vector in T.
Ax = b 可能没有solution
=> 变成这个更好 AtAx = Atb (best solution in this situation)
AtA不一定永远可逆
N(AtA) = N(A)
rank (AtA) = R(A)
AtA is invertible exactly if A has independent columns.
lecture 15:projections and least square
求b在a上面的投影p: (a,b是个向量)
正交 aT(b-xa) = 0
x = aTb/aTa
projection p = ax
p = a*aT/(aT*a) 是projection matrix
性质1:rank是1 因为是一行*一列得到的
性质2:Pt = P
性质3: P2 = P
Why project?
Because Ax = b may not have solution
solve Ax = p instead. p is the projection of b onto the column space. (等式右边是column space 的话肯定会有解)
AT(b-Ax_hat) = 0
=>ATAx = ATb
x = (ATA)-1ATb
p = A(ATA)-1ATb
projection matrix P = A(ATA)-1AT (不能再简化了,因为A不一定可逆,可能吧不是square matrix)
least square fitting by a line:
正交:
row space and null space 正交 orthogonal 因为A*x = 0
column space and null space of At 正交
Xt*y=0
subspace S is orthogonal to subspace T means that every vector in S is orthogonal to every vector in T.
Ax = b 可能没有solution
=> 变成这个更好 AtAx = Atb (best solution in this situation)
AtA不一定永远可逆
N(AtA) = N(A)
rank (AtA) = R(A)
AtA is invertible exactly if A has independent columns.
lecture 15:projections and least square
求b在a上面的投影p: (a,b是个向量)
正交 aT(b-xa) = 0
x = aTb/aTa
projection p = ax
p = a*aT/(aT*a) 是projection matrix
性质1:rank是1 因为是一行*一列得到的
性质2:Pt = P
性质3: P2 = P
Why project?
Because Ax = b may not have solution
solve Ax = p instead. p is the projection of b onto the column space. (等式右边是column space 的话肯定会有解)
AT(b-Ax_hat) = 0
=>ATAx = ATb
x = (ATA)-1ATb
p = A(ATA)-1ATb
projection matrix P = A(ATA)-1AT (不能再简化了,因为A不一定可逆,可能吧不是square matrix)
least square fitting by a line:
Friday, August 18, 2017
linear algebra 08/18/2017 lecture 12
lecture 12:
graph:
node - edge graph A (column 是 node; row 是edge)
现在看A的 null space
Euler's formula:
#nodes-#edges+#loops = 1
lecture 13:
u,v,w in Rt 构成一个 5*3 u rank = 3
N(u) = n-r = 0 只有零向量
r = m or r = n (full rank matrix )
graph:
node - edge graph A (column 是 node; row 是edge)
现在看A的 null space
Euler's formula:
#nodes-#edges+#loops = 1
lecture 13:
u,v,w in Rt 构成一个 5*3 u rank = 3
N(u) = n-r = 0 只有零向量
r = m or r = n (full rank matrix )
Thursday, August 17, 2017
linear algebra 08/17/2017 lecture 11
symmetric & upper triangular matrix = diagonal matrix. dimension = 3 in 3*3 matrix
Sum: symmetric or upper triangular matrix : take anything in S and anything in U. 不是并集,是相加。 所以可以得到all matrix. dimension (S+U) = 9 in 3*3 matrix
dim(S) +dim(U) = dim(S&U) + dim(S+U)
rank 1 matrix
example : A is 2*3 matrix
rank 1 matrix 像积木,eg. 一个rank 4 的matrix可以分解成4个rank 1 matrix的相乘
subset of rank 1 matrix can't form a sub space (两个rank 1 matrix相加可能得到一个rank 2 matrix)
In R4, V = [v1,v2,v3,v4], S is all v in R4 to make v1+v2+v3+v4 = 0
=>Av = 0 A = [1,1,1,1]
S 是A的null space. RA = 1 => S = R(N(A)) = n-r = 4-1 = 3
三个特殊解找出来即可
graph {nodes,edges}
Sum: symmetric or upper triangular matrix : take anything in S and anything in U. 不是并集,是相加。 所以可以得到all matrix. dimension (S+U) = 9 in 3*3 matrix
dim(S) +dim(U) = dim(S&U) + dim(S+U)
rank 1 matrix
example : A is 2*3 matrix
rank 1 matrix 像积木,eg. 一个rank 4 的matrix可以分解成4个rank 1 matrix的相乘
subset of rank 1 matrix can't form a sub space (两个rank 1 matrix相加可能得到一个rank 2 matrix)
In R4, V = [v1,v2,v3,v4], S is all v in R4 to make v1+v2+v3+v4 = 0
=>Av = 0 A = [1,1,1,1]
S 是A的null space. RA = 1 => S = R(N(A)) = n-r = 4-1 = 3
三个特殊解找出来即可
graph {nodes,edges}
Wednesday, August 16, 2017
linear algebra letcure 9 & 10 08/16/2017
lecture 9:
independence:
vector x1,x2,....xn are independent, if no combination gives 0 vector (except the 0 combinations.)
c1x1+c2x2+...+cnxn is not 0, they are independent
vectors v1,...vl span a space means: the space consists of all combinations of those vectors.
Basis for a space is a set of vectors with 2 properties:
1. they are independent.
2. they span the space
Example :
space is R3
one basis: [1;0;0] [0;1;0] [0;0;1]
n vectors give basis if the n*n matrix is invertible.
(n个vector的一种组合可以得到单元矩阵,也就是单元基basis)
every basis for the space has the same number of vectors.
It is called the dimension of the space.
rank(A) = #pivot column = dimension of the column space
dimension of null space is the number of free variables. = n - r
lecture 10:
4 subspace of A(m*n)
C(A) column space ;Rm
N(A) null space ;Rn
R(A) row space = all combination of columns of At C(At) ;Rn
N(At) :null space of At. The left null space of A ;Rm
basis? dimension?
C(A)
dimension of C(A) = r (rank of the matrix)
basis: is the pivot columns of A
R(A)
dimension of R(A) = r
N(A)
basis: special solutions
dimension: n-r
N(At)
basis: special solutions
dimension: m - r
why call it left null space?
At*y = 0 => yt*A = 0t =>左零矩阵
[A,I]=>[R,E]
如何计算y?
E*A = R
从E的最后一行找,因为E*A最后会得到一个最后一行为0的矩阵
independence:
vector x1,x2,....xn are independent, if no combination gives 0 vector (except the 0 combinations.)
c1x1+c2x2+...+cnxn is not 0, they are independent
vectors v1,...vl span a space means: the space consists of all combinations of those vectors.
Basis for a space is a set of vectors with 2 properties:
1. they are independent.
2. they span the space
Example :
space is R3
one basis: [1;0;0] [0;1;0] [0;0;1]
n vectors give basis if the n*n matrix is invertible.
(n个vector的一种组合可以得到单元矩阵,也就是单元基basis)
every basis for the space has the same number of vectors.
It is called the dimension of the space.
rank(A) = #pivot column = dimension of the column space
dimension of null space is the number of free variables. = n - r
lecture 10:
4 subspace of A(m*n)
C(A) column space ;Rm
N(A) null space ;Rn
R(A) row space = all combination of columns of At C(At) ;Rn
N(At) :null space of At. The left null space of A ;Rm
basis? dimension?
C(A)
dimension of C(A) = r (rank of the matrix)
basis: is the pivot columns of A
R(A)
dimension of R(A) = r
N(A)
basis: special solutions
dimension: n-r
N(At)
basis: special solutions
dimension: m - r
why call it left null space?
At*y = 0 => yt*A = 0t =>左零矩阵
[A,I]=>[R,E]
如何计算y?
E*A = R
从E的最后一行找,因为E*A最后会得到一个最后一行为0的矩阵
Monday, August 14, 2017
linear algebra 08/14/2017 lecture 7 & 8
lecture 7:
the rank of the matrix. 矩阵的秩
do elimination, find the pivot columns and free columns.
pivot variables + free variables = n (column number)
reduced row echelon form 是一种矩阵的继续简化
求解null space
解法1:produce null space matrix R*N=0
R是已经被简化的矩阵,变成[I,F;0;0] I 是单元矩阵
N=[-F;I]
解法2:求解null space.把free variable 其中一个设为1,其余free variable 为0. 然后求出一组解,
lecture 8:
Ax = b
solvable when b is in C(A)
If a combination of rows of A gives 0 rows,
to find a compete solutions
1.x particular (找一个特殊解): set all free variables as 0
2. 再把其中一个free variable 换成1,其余的为0,求几组特殊解
The case of full column rank
r = n
what that imply about the solutions? What is that mean?
No free variables
=> N(A) = {0} null space only have 零向量
solution to Ax = b
x = unique solution, if exists (0 or 1 solution)
full row rank means
r = m
can solve Ax = b for every b.
free variables n -r = n-m 个
肯定可以得出一个最简矩阵R=[I F]
special case: r = m = n
R = I
=> N(A) = {0} null space only have 零向量
r<m, r<n
R = [I,F;0,0]
=> 0 or infinite solutions
the rank of the matrix. 矩阵的秩
do elimination, find the pivot columns and free columns.
pivot variables + free variables = n (column number)
reduced row echelon form 是一种矩阵的继续简化
求解null space
解法1:produce null space matrix R*N=0
R是已经被简化的矩阵,变成[I,F;0;0] I 是单元矩阵
N=[-F;I]
解法2:求解null space.把free variable 其中一个设为1,其余free variable 为0. 然后求出一组解,
lecture 8:
Ax = b
solvable when b is in C(A)
If a combination of rows of A gives 0 rows,
to find a compete solutions
1.x particular (找一个特殊解): set all free variables as 0
2. 再把其中一个free variable 换成1,其余的为0,求几组特殊解
The case of full column rank
r = n
what that imply about the solutions? What is that mean?
No free variables
=> N(A) = {0} null space only have 零向量
solution to Ax = b
x = unique solution, if exists (0 or 1 solution)
full row rank means
r = m
can solve Ax = b for every b.
free variables n -r = n-m 个
肯定可以得出一个最简矩阵R=[I F]
special case: r = m = n
R = I
=> N(A) = {0} null space only have 零向量
Ax = b
r= m < n
R= [I;0] => 0 or 1 solution
r = m<n
R = [I F] => infinite solution
R = [I,F;0,0]
=> 0 or infinite solutions
Sunday, August 13, 2017
linear algebra notes 08//13/2017 lecture 5 & 6
lecture 5:
LU 分解的意义:
http://blog.csdn.net/carrierlxksuper/article/details/8487276
permutation:
P-1 = Pt
一共n!个permutation matrix
transpose 的概念
symmetric matrix:
At = A
Rt*R is always symmetric.
WHY? Take transpose!
(RtR)t = Rt*Rtt = Rt*R (和逆矩阵的公式很像 (AB)-1 = B-1A-1)
所以这个是symmetric的
Vector space
Example: R2 = all 2 dimensional vectors
a vector space inside R2 is : a subspace of R2
一定得过零点
subspace of R2
1. all of R2 (最大子空间)
2. any lines through [0;0]
3. zero vector only (最小子空间)
子空间 补充:https://www.zhihu.com/question/48849797
column space: columns in Rn. Add their combinations form a subspace . (满足定义)
lecture 6:
Ax=b 有解 当b in A的column spaces (根据定义来的)
主列
null space (零空间) of A
all vectors x to let Ax = 0
at least contains [0;0;0]
solutions to Ax = 0 always gives a subspace.
subspace 一定会过零点
LU 分解的意义:
http://blog.csdn.net/carrierlxksuper/article/details/8487276
permutation:
P-1 = Pt
一共n!个permutation matrix
transpose 的概念
symmetric matrix:
At = A
Rt*R is always symmetric.
WHY? Take transpose!
(RtR)t = Rt*Rtt = Rt*R (和逆矩阵的公式很像 (AB)-1 = B-1A-1)
所以这个是symmetric的
Vector space
Example: R2 = all 2 dimensional vectors
a vector space inside R2 is : a subspace of R2
一定得过零点
subspace of R2
1. all of R2 (最大子空间)
2. any lines through [0;0]
3. zero vector only (最小子空间)
子空间 补充:https://www.zhihu.com/question/48849797
column space: columns in Rn. Add their combinations form a subspace . (满足定义)
lecture 6:
Ax=b 有解 当b in A的column spaces (根据定义来的)
主列
null space (零空间) of A
all vectors x to let Ax = 0
at least contains [0;0;0]
solutions to Ax = 0 always gives a subspace.
subspace 一定会过零点
Friday, August 11, 2017
MIT linear algebra course note
08/11/2017 lecture 1 & 2
1. permutation matrix
2. inverse matrix E*E-1 = I
3. identity matrix
4. 如何做矩阵变换。E*A=B 使得 第二行substract 第一行
08/12/2017 lecture 3&4
4种方法计算矩阵乘法:
1. 正常法,每个值都是1 row * 1 column
2. column way. A乘以B的每个column
3. row way. A的每个row 乘以B
4. A的每个column 乘以 B的每个row。加在一起
5. cut matrix into blocks。 然后把每个block之间进行运算
A的左逆 矩阵和右逆矩阵是相同的 if matrix is invertible (non singular)
Singular case (no inverse)
比如[1,3;2,6]
singular matrix can get 0 by some matrix x
Ax = 0 if A is singular matrix. x 是存在的
A times B的一列j,得到的是结果的C的一列j
A的一行j times B,得到的是结果的C的一行j
Gauss - Jordan (solve 2 equations at once)
[A,I]--->[I,A-1]


AB 的逆矩阵 = B-1A-1
矩阵的转置
(A-1)t = (At)-1
A 的逆矩阵的转置是A的转置的逆矩阵
A= LU
if there is no row exchange, the multiplers will directly go into L
how many operations on n *n matrix?
n^3
permutation:
可以在单元矩阵中变换
http://blog.csdn.net/lc013/article/details/52244464
https://github.com/mebusy/notes/blob/master/dev_notes/LinearAlgebra.md
1. permutation matrix
2. inverse matrix E*E-1 = I
3. identity matrix
4. 如何做矩阵变换。E*A=B 使得 第二行substract 第一行
08/12/2017 lecture 3&4
4种方法计算矩阵乘法:
1. 正常法,每个值都是1 row * 1 column
2. column way. A乘以B的每个column
3. row way. A的每个row 乘以B
4. A的每个column 乘以 B的每个row。加在一起
5. cut matrix into blocks。 然后把每个block之间进行运算
A的左逆 矩阵和右逆矩阵是相同的 if matrix is invertible (non singular)
Singular case (no inverse)
比如[1,3;2,6]
singular matrix can get 0 by some matrix x
Ax = 0 if A is singular matrix. x 是存在的
A times B的一列j,得到的是结果的C的一列j
A的一行j times B,得到的是结果的C的一行j
Gauss - Jordan (solve 2 equations at once)
[A,I]--->[I,A-1]


AB 的逆矩阵 = B-1A-1
矩阵的转置
(A-1)t = (At)-1
A 的逆矩阵的转置是A的转置的逆矩阵
A= LU
if there is no row exchange, the multiplers will directly go into L
how many operations on n *n matrix?
n^3
permutation:
可以在单元矩阵中变换
原矩阵乘以这个矩阵(permuatation matrix)表示第二行第三行互换
permutation matrix : p-1 = pt 如果第二行和第三行 换了,那么再换一次第二行和第三行就是还是原来的矩阵
置换矩阵(Permutation matrix):矩阵的每一行和每一列的元素中只有一个1,其余元素都为0。(不严谨的解释)
转置矩阵(Transpose matrix):矩阵的行变成对应的列,矩阵的列变成对应的行。(不严谨的直白解释)
性质:置换矩阵(P)的逆是其(置换矩阵自己的)转置(T),
即:P^(-1)= P^T
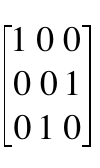
如:3×3的置换矩阵群(共3! = 6个,补充4×4的置换矩阵共4! = 4×3×2×1 = 24个)
1 0 0 | 0 1 0
0 1 0 | 1 0 0
0 0 1 | 0 0 1
----------------
0 0 1 | 1 0 0
0 1 0 | 0 0 1
1 0 0 | 0 1 0
置换矩阵的逆=置换矩阵的转置(上面4个置换矩阵的转置矩阵都是自身,又因为他们的逆=他们的转置,所以他们的逆=自身)
0 1 0 | 0 0 1
0 0 1 | 1 0 0
1 0 0 | 0 1 0
置换矩阵的逆=置换矩阵的转置(这两个矩阵的转置=对方,因此这两个矩阵的逆=对方)
LU分解
LU分解是指,把矩阵分解为 消元矩阵E 的逆操作 L(下三角)
和 A 被消元后的结果矩阵 U(上三角)的乘积.
- LU分解不借助 行交换的关键是是 中间不能出现 0 pivot
- 但是对最后一个 pivot 没有 非0的要求
- 因为奇异矩阵也有LU分解
http://blog.csdn.net/lc013/article/details/52244464
https://github.com/mebusy/notes/blob/master/dev_notes/LinearAlgebra.md
Subscribe to:
Comments (Atom)